¶ Data Sufficiency
Quick Overview of the general approach that is followed by examinees for answering DS questions:-
While the genre of Data Sufficiency is unique, the structure is not – all Data Sufficiency questions are structured exactly the same, with three key elements: the question stem (which may or may not contain important facts), the statements (always two statements), and the answer choices (which are always exactly the same). Consider this example to see what a Data Sufficiency question will look like:
By what percent was the price of a certain candy bar increased?
(1) The price of the candy bar was increased by 5 cents.
(2) The price of the candy bar after the increase was 45 cents.
(A) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
(B) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
(C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(D) EACH statement ALONE is sufficient.
(E) Statements (1) and (2) TOGETHER are NOT sufficient.
Read the question stem. If it needs some rephrasing of the question to help you understand it better, do it right away.
Look at statement 1. Is it sufficient alone? Two possible answers - Yes or No
Yes - Answer is either A or D. Write down A/D on your paper. Go back and read the question stem again. (This step is to forget what you read in statement 1 and keep an eye on the question.) Read statement 2. Is it sufficient alone? If yes, answer is D. If no, answer is A.
No - Answer is either B, C or E. Write down B/C/E on your paper. Go back and read the question stem again. Read statement 2. Is it sufficient alone? If yes, answer is B. Move on to the next question. If No, consider both statements together now. Are they sufficient now? If Yes, answer is C else it is E.
- A statement is sufficient when it guarantees exactly one (and only one) answer to the question.
- This means that in a Yes/No question, you have sufficient information if the answer is “Definitely Yes” or if the answer is “Definitely No”. You do not have sufficient information when the answer is “Sometimes Yes but Sometimes No” (or “Maybe”).
- This means that in a “What is the Value?” question, you have sufficient information when you can pin down exactly one value for the question, but you do not have sufficient information when more than one value is possible.
Introduction to Data Sufficiency:
Top five tips for Data Sufficiency
1. Don't waste your time solving the problem :Data sufficiency questions aren't about giving the solution to the problem, they're about determining whether there is enough information for you to be able to answer the question. Don't start by solving the problem.
2. Memorize the answer choices :In data sufficiency questions, the five answer choices are always the same. Memorizing these will speed up your response. These are: -
A. Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.
B. Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.
C. Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.
D. Each statement alone is sufficient to answer the question.
E. Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.
3. Consider each statement separately :Look at each statement, and see if it gives you enough information alone.
4. Make sure the solution answers the question that is asked: Be sure that the answer is sufficient to the question.
5. Brush up on your math: As with many quantitative questions on the IBA admission test, having a good grasp of mental math will speed up your response.
Overall Dos and Don’ts on DS Questions
Dos:
1. Remember the cardinal rule of DS – Evaluate the individual statement alone; only when you know that they are insufficient can you combine the data given in the statements.
2. Always look for a unique answer for the question asked.
3. Do not try to find the exact answer in all DS questions. Stop at the stage where you know for sure that a certain piece of information is sufficient.
4. Read the question statement carefully and do not miss out on reading the entire statement.
5. Pay attention to vital cues like numbers, constraints and keywords. Remember that every word on a IBA question may have an implication.
6. Quickly jot down important information/constraints/keywords as you read the question.
7. Deconstruct the question – this means converting the question to a simpler version of itself which will tell you what data to look for in the statements.
8. In questions on Algebra, develop variables, expressions and equations based on the Question data.
9. In questions on Geometry, draw the figure if it’s not given. If the figure is given, redraw the figure in such a way that YOU will understand.
10. Learn to eliminate options at different stages using the AD/BCE technique.
How to answer data sufficiency more accurately and efficiently:
Don’ts:
1. Do not skip/overlook any information (very obvious, right?).
2. Do not make assumptions. For example, a number need not necessarily be a positive integer.
3. Do not attempt to solve the whole question mentally – this can be very taxing and can drain you out very quickly.
4. Do not combine the statements until you have made sure that they are insufficient when considered individually.
5. Do not start analyzing the statements before de-constructing the question stem.
6. Do not forget the importance of the number 0 in questions on inequalities.
7. Do not combine the statements if you see a pair of linear equations, without testing them individually.
8 . Do not forget that a perfect square can have both negative and positive roots.
Sample Question
- A certain plumber charges $92 for each job completed in 4 hours or less and $23 per hour for each job completed in more than 4 hours. If it took the plumber a total of 7 hours to complete two separate jobs, what was the total amount charged by the plumber for the two jobs? (1) The plumber charged $92 for one of the two jobs. (2) The plumber charged $138 for one of the two jobs.
- Is the positive two-digit integer N less than 40 ? ( 1) The units digit of N is 6 more than the tens digit. (2) N is 4 less than 4 times the units digit
- What is the number of cans that can be packed in a certain carton? (1) The interior volume of this carton is 2,304 cubic inches. (2) The exterior of each can is 6 inches high and has a diameter of 4 inches.
- Material A costs $3 per kilogram, and Material B costs $5 per kilogram. If 10 kilograms of Material K consists of x kilograms of Material A and y kilograms of Material B, is x > y? (1) Y> 4 (2) The cost of the 10 kilograms of Material K is less than $40.
Question Topics
Numbers Theory
- What is the remainder when m is divided by 3? (1) The remainder when m is divided by 6 is 2. (2) The remainder when m is divided by 12 is 2.
- Is m divisible by n? (1) m + n is divisible by m – n. (2) m + n is divisible by n
- Is n an integer? (1) n3 + 3n is an integer. (2) n4 + 4n is an integer.
Average
- What is the average of the consecutive integers m through n, inclusive? (1) The average of m and n is 23.5. (2) The average of the integers between m and n not including either is 23.5.
- A class consists of boys and girls only. On a final exam in History, the average score of the girls is 72 and the average score of the boys is 70. Is the average score of the class 71? (1) Smith is one of the classmates and Smith has the same number of boy classmates as girl classmates. (2) The number of students in the class is 101.
Fractions
- What fraction of the students in a class have blue eyes? (1) 10% of the girls have blue eyes. (2) 20% of the boys have blue eyes.
- In a country, 65% of male citizen and 68% of female citizen are eligible to vote. What fraction of the citizens voted during the election? (1) 68% of male citizens eligible to vote voted. (2) 65% of female citizens eligible to vote voted
Inequalities
- Is x + y > 6? (1) x + 2y > 8 (2) 2x + y > 8
- Is (ab)2 > ab ? (1) a + 3 = b + 6 = 0 (2) 0 > a > b
Ratio and Proportion
- The savings from a person’s income is the difference between his or her income and expenditure. What is the ratio of Mr. Kelvin’s savings in the year 1998 to the year 1999? (1) The ratio of his income in the years 1998 to 1999 is 3 : 4. (2) The ratio of his expenditure in the years 1998 to 1999 is 5 : 6
- All the clients that Company Daraz had at the beginning of last year remained with the company for the whole year. If Company Daraz acquired new clients during the year, what was the ratio of the number of clients that Company Daraz had at the end of last year to the number of clients that it had at the beginning of last year? (1) The ratio of the number of clients that Company Daraz had at the beginning of last year to the number of new clients that it acquired during the year was 12 to 1. (2) Company Daraz had 144 clients at the beginning of last year.
- A farmer has a total of 60 pigs, cows, and horses on his farm. How many pigs does he have? (1) The ratio of horses to cows is 2:9. (2) He has more than 36 cows.
- At a certain baseball game, each of the spectators is either a Bullfrogs fan or a Chipmunks fan, and no one is both. What is the ratio of Bullfrogs fans to Chipmunks fans among spectators at the baseball game? (1) The number of Chipmunks fans among the spectators is 20% greater than the number of Bullfrogs fans. (2) The total number of spectators at the baseball game is 4,400.
- In the first hour of a bake sale, students sold either cheese cakes, which sold for $1.30, or pastries, which sold for $1.50. What was the ratio of cheese cakes sold to pastries sold during that hour? (1) The average price for the items sold during that hour was $1.42. (2) The total price for all items sold during that hour was $14.20.
Percentage + Sets
- In a taste test conducted for coffee brands X and Y, if each of the 1,600 people polled voted for either X or Y (but not both), what percent of the males voted for brand Y? (1) Forty percent of the females polled voted for brand X. (2) Sixty-five percent of the males voted for brand X.
- Of the people who attended a workshop, 60 percent were teachers and some of the teachers were teachers of language arts. What percent of the people who attended the workshop were teachers of language arts? (1) 200 people attended the workshop. (2) 72 of the teachers who attended the workshop were not teachers of language arts.
- Every man in a certain class either belongs to group A, belongs to group B, or belongs to both groups. 20% of group A consists of men and 65% of group B consists of men. What percentage of the two groups together is made up of men? (1) Group A contains 50 people. (2) Group B contains 100 people.
- How many people in a group of 50 own neither a fax machine nor a laser printer? (1) The total number of people in the group who own a fax machine or a laser printer or both is less than 50. (2) The total number of people in the group who own both a fax machine and a laser printer is 15.
- Of a group of 50 households, how many have at least one cat or at least one dog, but not both? (1) The number of households that have at least one cat and at least one dog is 4. (2) The number of households that have no cats and no dogs is 14
Probability
- What is the probability that a person selected randomly from a group of people is a woman in pink attire? (1) Of the women in the group, 4% are wearing pink attire. (2) Of the people in the group, 40% are women
- Each of the marbles in a jar is either red or white or blue. If one marble is to be selected at random from the jar, what is the probability that the marble will be blue? (1) There are a total of 24 marbles in the jar, 8 of which are red. (2) The probability that the marble selected will be white is ½
- In a real estate office that employs n salespeople, 306 of them are females and x of the females are new employees. What is the value of n? (1) If an employee were randomly selected from the n employees, the probability of selecting a 2 female would be 3 . (2) If an employee were randomly selected from the female employees, the probability of selecting a 1 new employee would be 2 .
Algebra
- x is how many times y if y ≠ 0? (1) x/y + y/(x-2y) = 0 (2) x = 2y /(x + y)
- If r > 0 and s > 0, is r/s > s/r? (1) r/3s = ¼ (2) s=r+4
- Robin invested a total of $12,000 in two investments, X and Y, so that the investments earned the same amount of simple annual interest. How many dollars did Robin invest in investment Y ? (1) Investment X paid 3 percent simple annual interest, and investment Y paid 6 percent simple annual interest. (2) Robin invested more than $1,000 in investment X.
Distance/Time/Speed
1. If it took Carlos 1/2 hour to cycle from his house to the library yesterday, was the distance that he cycled greater than 6 miles? (Note: 1 mile = 5280 ft) (1) The average speed at which Carlos cycles from his house to the library yesterday was greater than 16 feet per second (2) The average speed at which Carlos cycles from his house to the library yesterday was less than 18 feet per second.
2. Starting from the same point, a sparrow and a hawk flew in opposite directions. Each traveled at a constant speed until they were 200 feet apart. How far did the sparrow travel? (1) The ratio of the sparrow’s speed to the hawk’s speed was 3 to 2. (2) The average speed of the sparrow was 5 feet per second faster than the average speed of the hawk.
3. Carlotta can drive from her home to her office by one of two possible routes. If she must also return by one of these routes, what is the distance of the shorter route? (1) When she drives from her home to her office by the shorter route and returns by the longer route, she drives a total of 42 kilometers. (2) When she drives both ways, from her home to her office and back, by the longer route, she drives a total of 46 kilometers.
Geometry
- In the figure below, point D is on AC . What is the degree measure of ^BAC ? (1) The measure of ^BDC is 60° . (2) The degree measure of ^BAC is less than the degree measure of ^BCD.
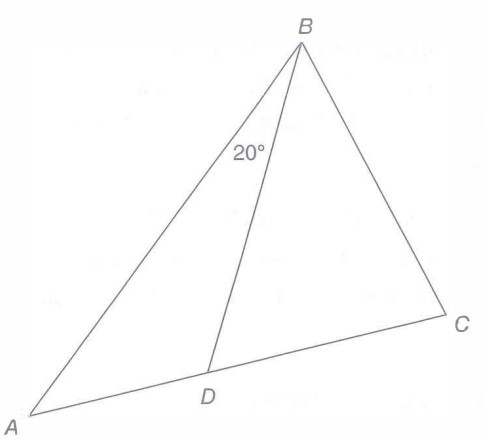
2. In cross section, a tunnel that carries one lane of one-way traffic is a semicircle with radius 4.2 m. Is the tunnel large enough to accommodate the truck that is approaching the entrance to the tunnel? (1) The maximum width of the truck is 2.4 m. (2) The maximum height of the truck is 4 m.
3.

Is ABC an equilateral triangle? (1) BD/AD = DC/DB (2) AB2 + CD2= AD2 + BC2
4. A ladder leans against a vertical wall. The base of the ladder is 15 feet away from the wall and the top of the ladder is 20 feet above the ground on the wall. The wall is perpendicular to the ground. The ladder is pulled farther from the wall causing the top of the ladder to fall by x feet. How far away was the base of the ladder moved? (1) x = 1. (2) The length of the ladder is 25 feet.